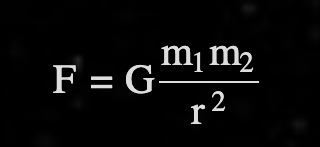The N-body Problem
Background: The n-body problem describes the motion of any "n" objects when under each others gravitational field. As described by Brittanica: "In the general n-body problem, all bodies have arbitrary masses, initial velocities, and positions; the bodies interact through Newton's law of gravitation, and one attempts to determine the subsequent motion of all the bodies." This theoretical equation is closely linked with the motion of celestial bodies, leading to centuries of research and testing to find a general solution. Although many approximations have been found (such as restricted 3-body problems of Jupiter's effect on asteroids), an exact general equation has yet to be discovered.
(Source: Brittanica: The n-body problem)
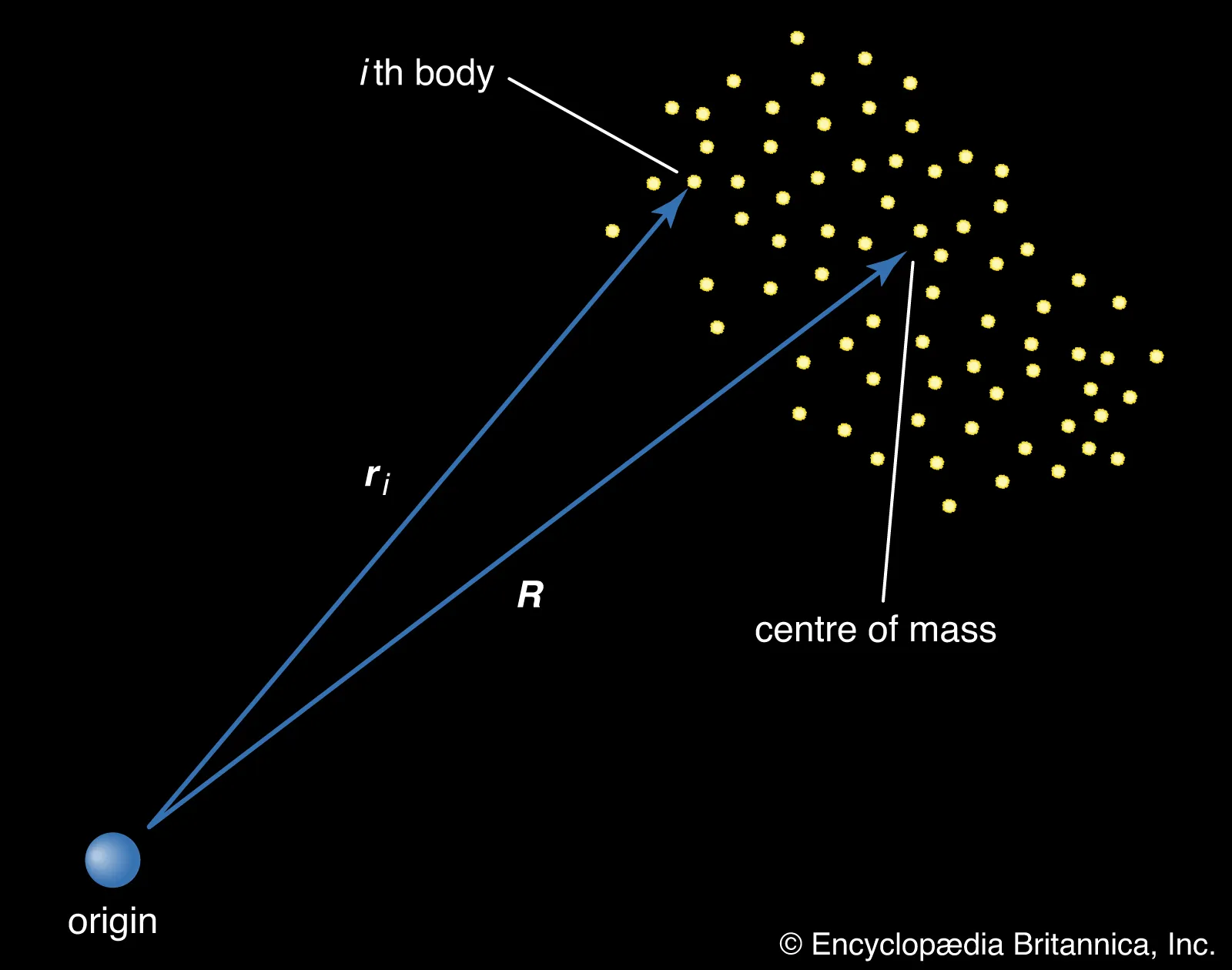
Inspiration: Our team was inspired by the recent special relativity units in the UNC physics classes, and wanted to explore more into influential physics problems. We hope to contribute our visualizations to the body of n-body research in the hopes that a general solution will be found.